In this tutorial you will do the following.
Revise gas expansions in turbines.
Revise the Joule cycle.
Study the Joule cycle with friction.
Extend the work to cycles with heat exchangers.
Solve typical exam questions.
1. Revision of Expansion And Compression Process
When a gas is expanded from pressure p1 to pressure p2 adiabatically, the temperature ratio
is given by the formula
is given by the formula

The same formula may be applied to a compression process. Always remember that when a
gas is expanded it gets colder and when it is compressed it gets hotter. The temperature
change is T2 - T1
gas is expanded it gets colder and when it is compressed it gets hotter. The temperature
change is T2 - T1
If there is friction the isentropic efficiency (ηis) is expressed as
ηis = ∆T (ideal)/∆T(actual) for a compression.
ηis = ∆T (actual)/∆T(ideal) for an expansion.
ηis = ∆T (ideal)/∆T(actual) for a compression.
ηis = ∆T (actual)/∆T(ideal) for an expansion.
An alternative way of expressing this is with POLYTROPIC EFFICIENCY η∞
For a compression from (1) to (2) the temperature ratio is expressed as follows.
For a compression from (1) to (2) the temperature ratio is expressed as follows.
and for an expansion from (1) to (2)
where η∞ is called the polytropic efficiency.
where η∞ is called the polytropic efficiency.
Worked Example No.1
A gas turbine expands 4 kg/s of air from 12 bar and 900oC to 1 bar adiabatically with
an isentropic efficiency of 87%. Calculate the exhaust temperature and the power
output. γ = 1.4 cp = 1005 J/kg K
Solution
T2 = T1 (1/12)1-1/1.4 = 1173 (1/12)0.2958 = 562.48 K
Ideal temperature change = 1173 - 562.48 = 610.52 K
Actual temperature change = 87% x 610.52 = 531.15 K
Exhaust temperature = 1173 - 531.15 = 641.85 K
The steady flow energy equation states
Φ + P = change in enthalpy/s
Since it is an adiabatic process Φ = 0 so
P = ∆H/s = m cp ∆T = 4 x 1005 x (531.15)
P = - 2.135 x 106 W (Leaving the system)
P(out) = 2.135 MW
T2 = T1 (1/12)1-1/1.4 = 1173 (1/12)0.2958 = 562.48 K
Ideal temperature change = 1173 - 562.48 = 610.52 K
Actual temperature change = 87% x 610.52 = 531.15 K
Exhaust temperature = 1173 - 531.15 = 641.85 K
The steady flow energy equation states
Φ + P = change in enthalpy/s
Since it is an adiabatic process Φ = 0 so
P = ∆H/s = m cp ∆T = 4 x 1005 x (531.15)
P = - 2.135 x 106 W (Leaving the system)
P(out) = 2.135 MW
Self Assessment Exercise No.1
1. A gas turbine expands 6 kg/s of air from 8 bar and 700oC to 1 bar isentropically.
Calculate the exhaust temperature and the power output. γ = 1.4 cp = 1005 J/kg K
(Answers 537.1 K and 2.628 MW)
1. A gas turbine expands 6 kg/s of air from 8 bar and 700oC to 1 bar isentropically.
Calculate the exhaust temperature and the power output. γ = 1.4 cp = 1005 J/kg K
(Answers 537.1 K and 2.628 MW)
2. A gas turbine expands 3 kg/s of air from 10 bar and 920oC to 1 bar adiabatically with
an isentropic efficiency of 92%. Calculate the exhaust temperature and the power
output. γ = 1.41 cp = 1010 J/kg K
(Answers 657.3 K and 1.62 MW)
an isentropic efficiency of 92%. Calculate the exhaust temperature and the power
output. γ = 1.41 cp = 1010 J/kg K
(Answers 657.3 K and 1.62 MW)
3. A gas turbine expands 7 kg/s of air from 9 bar and 850oC to 1 bar adiabatically with an
isentropic efficiency of 87%. Calculate the exhaust temperature and the power output.
γ = 1.4 cp = 1005 J/kg K
(Answers 667.5 K and 3.204 MW)
isentropic efficiency of 87%. Calculate the exhaust temperature and the power output.
γ = 1.4 cp = 1005 J/kg K
(Answers 667.5 K and 3.204 MW)
2. The Basic Gas Turbine Cycle
The ideal and basic cycle is called the JOULE cycle and is also known as the constant
pressure cycle because the heating and cooling processes are conducted at constant
pressure. A simple layout is shown on fig. 1.
 Figure 1 Illustrative diagram.
Figure 1 Illustrative diagram.The cycle in block diagram form is shown on fig. 2.

Fig.2 Block diagram
There are 4 ideal processes in the cycle.
1 - 2 Reversible adiabatic (isentropic) compression requiring power input.
Pin= ∆H/s = m cp (T2-T1)
There are 4 ideal processes in the cycle.
1 - 2 Reversible adiabatic (isentropic) compression requiring power input.
Pin= ∆H/s = m cp (T2-T1)
2 - 3 Constant pressure heating requiring heat input.
Φin = ∆H/s = m cp (T3-T2)
Φin = ∆H/s = m cp (T3-T2)
3 - 4 Reversible adiabatic (isentropic) expansion producing power output.
Pout = ∆H/s = m cp (T3-T4)
Pout = ∆H/s = m cp (T3-T4)
4 - 1 Constant pressure cooling back to the original state requiring heat removal.
Φ out = ∆H/s = m cp (T4-T1)
Φ out = ∆H/s = m cp (T4-T1)
The pressure - volume, pressure - enthalpy and temperature-entropy diagrams are shown on
figs. 3a, 3b and 3c respectively.
figs. 3a, 3b and 3c respectively.
Fig 3 p-V diagram, p-h diagram, T-s diagram
2.1 EFFICIENCY
The efficiency is found by applying the first law of thermodynamics
The efficiency is found by applying the first law of thermodynamics
It assumed that the mass and the specific heats are the same for the heater and cooler.
It is easy to show that the temperature ratio for the turbine and compressor are the same.
It is easy to show that the temperature ratio for the turbine and compressor are the same.
rp is the pressure compression ratio for the turbine and compressor.
This shows that the efficiency depends only on the pressure ratio which in turn affects the
hottest temperature in the cycle.
hottest temperature in the cycle.
Worked Example No.2
A gas turbine uses the Joule cycle. The pressure ratio is 6/1. The inlet temperature to
the compressor is 10oC. The flow rate of air is 0.2 kg/s. The temperature at inlet to the
turbine is 950oC. Calculate the following.
i. The cycle efficiency.
ii. The heat transfer into the heater.
iii. The net power output.
γ = 1.4 cp = 1.005 kJ/kg K
A gas turbine uses the Joule cycle. The pressure ratio is 6/1. The inlet temperature to
the compressor is 10oC. The flow rate of air is 0.2 kg/s. The temperature at inlet to the
turbine is 950oC. Calculate the following.
i. The cycle efficiency.
ii. The heat transfer into the heater.
iii. The net power output.
γ = 1.4 cp = 1.005 kJ/kg K
Solution
Self Assessment Exercise No.2
A gas turbine uses the Joule cycle. The inlet pressure and temperature to the
compressor are respectively 1 bar and -10oC. After constant pressure heating, the
pressure and temperature are 7 bar and 700oC respectively. The flow rate of air is 0.4
kg/s. Calculate the following.
1. The cycle efficiency.
2. The heat transfer into the heater.
3. the nett power output.
γ = 1.4 cp = 1.005 kJ/kg K
(Answers 42.7 % , 206.7 kW and 88.26 kW)
A gas turbine uses the Joule cycle. The inlet pressure and temperature to the
compressor are respectively 1 bar and -10oC. After constant pressure heating, the
pressure and temperature are 7 bar and 700oC respectively. The flow rate of air is 0.4
kg/s. Calculate the following.
1. The cycle efficiency.
2. The heat transfer into the heater.
3. the nett power output.
γ = 1.4 cp = 1.005 kJ/kg K
(Answers 42.7 % , 206.7 kW and 88.26 kW)
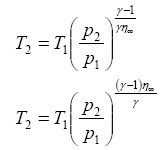






No comments:
Post a Comment